Reales Freitagabend-Problem bei der Essensplanung. Meine Begleiter schauen mich bestürzt an: „Das kann ich noch nicht mal mit dem Taschenrechner ausrechnen, irgendwas mit Pi. Ich kann kein Mathe!“ — Ich rolle mit den Augen und verkünde das Ergebnis. „Ui. Das müssen wir Dir jetzt einfach so glauben.“ … Ich drohe postwendend an, einen Blog-Beitrag darüber zu schreiben, wie man auch ohne zehn Nachkommastellen von Pi auf die Lösung kommt.
Merke: Das große Alphabet und das kleine Einmaleins bringen einen weit im Leben. Das konkrete Problem ist viel, viel einfacher, als einem die anerzogene Mathephobie glauben macht.
Betrachten wir einfach mal quadratische Blechpizza statt runde Pizza-Pies – „Pie“ wie englisch „Torte“, nicht wie die Zahl „Pi“.
„Aber, aber, aber … !“
Ja, ja, ganz unten im Beitrag komme ich noch auf die Zahl Pi. — Spoiler-Alert: Völlig irrelevant für das konkrete Problem.
Also – wir betrachten eine idealisiert quadratische Blechpizza. Eine Mini-Blechpizza für eine Maus mit 1 cm = Zentimeter Kantenlänge. Oder ein kleines Pizzastück mit 10 cm Kantenlänge – bzw. 1 dm = Dezimeter. Oder ein Rummelplatz-Pizzablech mit 1 m = Meter Kantenlänge. Es geht mir hier um die Zahl „1“.

Mäusepizza mit 1 cm Kantenlänge,
Pizza-Stück mit 1 dm Kantenlänge,
Rummelplatz-Pizza mit 1 m Kantenlänge
(nicht maßstabsgetreu)
Die Rummelplatz-Pizza mit 1 m Kantenlänge ist 1 qm = Quadratmeter groß. Wie groß ist denn aber eine quadratische Blech-Pizza mit 2 m Kantenlänge? Ist sie nur doppelt so groß?
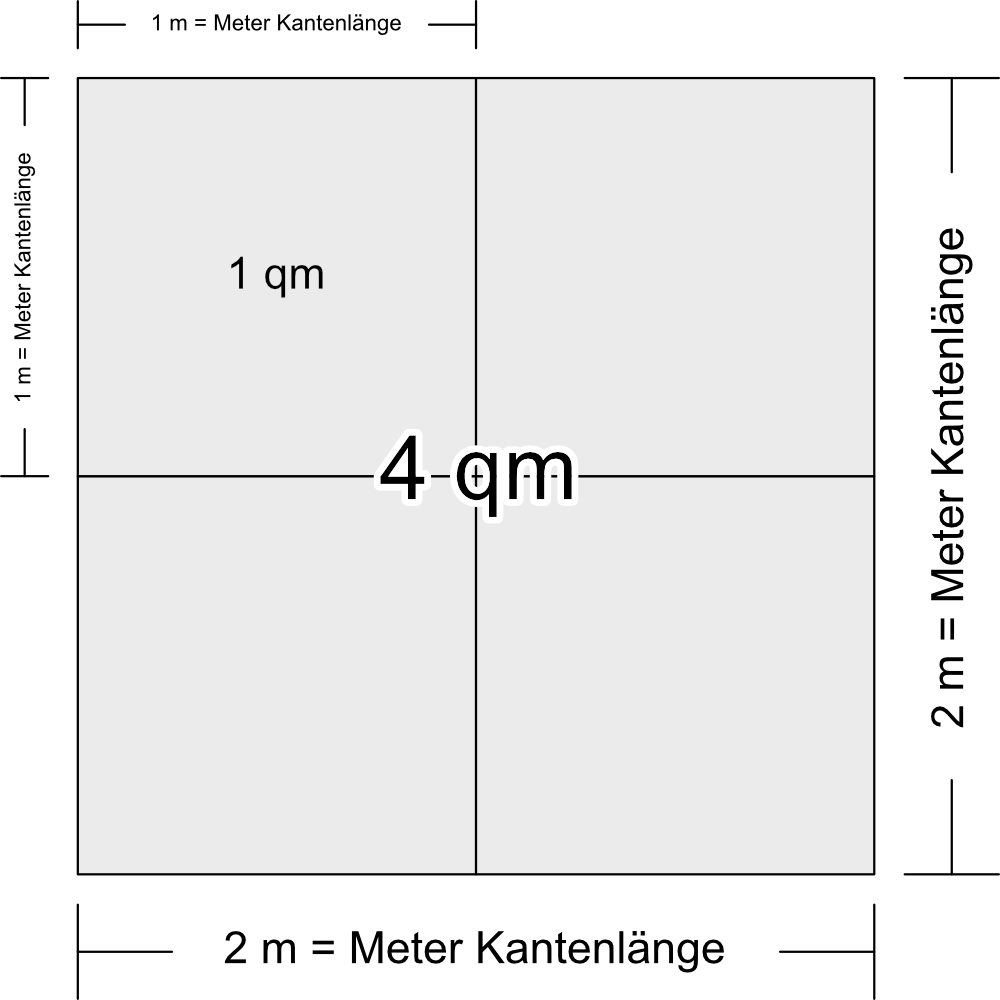
Nein, siehe Skizze: Wir legen vier 1×1 m Pizzen quadratisch aneinander, damit ist sie logischerweise 4 mal so groß: 2 m Kantenlänge mal 2 m Kantenlänge sind 4 qm. … Und wie steht es mit einer quadratischen Pizza mit 3 m Kantenlänge?
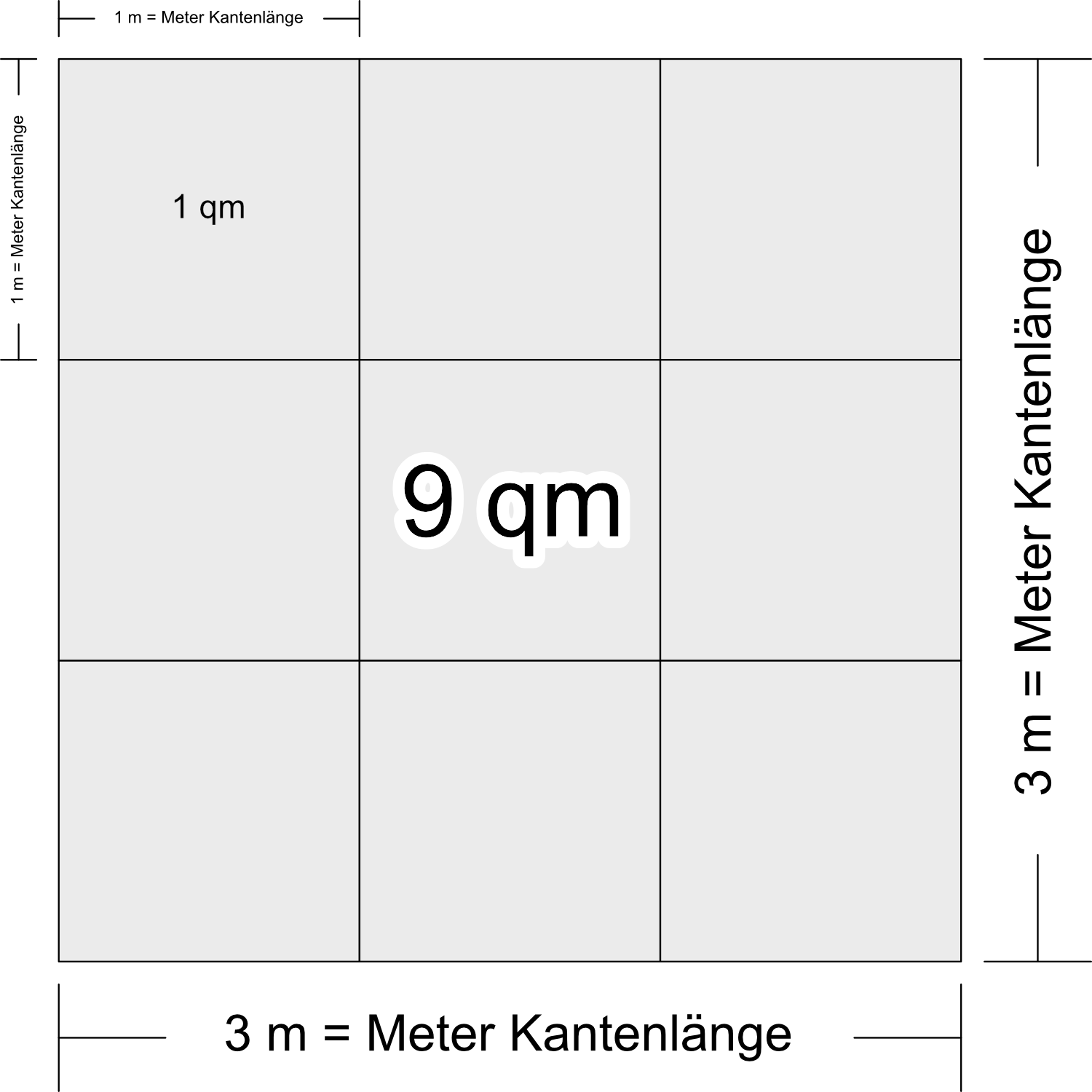
Siehe Skizze: Sie ist nicht 3 mal so groß, sie ist 3×3, also 9 mal so groß. — Merke: Die Größe der Pizza in qm = Quadratmetern ist quadratisch (oha!) zu ihrer Kantenlänge. Eine 1 m große quadratische Pizza hat 1 qm, bei 2 m Kantenlänge sind es 2×2 = 4 qm, bei 3 m Kantenlänge sind es 9 qm. … Und so weiter.
Es ist dabei egal, ob es sich um Meter, Dezimeter, Zentimeter oder was immer für XYZ-Meter handelt: Die Mäusepizza beispielsweise mit 1 cm Kantenlänge ist 1 qcm („Quadratzentimeter“) groß, bei 2 cm sind es 4 qcm, bei 3 cm sind es 9 qcm. … Und so weiter.
Zusammengefasst: Was wissen wir bis hier? Die Fläche der quadratischen Pizza ist quadratisch zu ihrer Kantenlänge. Dahinter stehende Nullen, Stichwort: „10 cm sind 1 dm“ können wir getrost ignorieren.
Zurück zu unserer 40er und 60er Pizza – ja, ja, die sind rund, aber nehmen wir aktuell mal an, das seien quadratische Blechpizzen. Also haben wir eine Pizza mit 60 cm bzw. 6 dm Kantenlänge und eine mit 40 cm bzw. 4 dm Kantenlänge.
- Die quadratische 6 dm-Pizza ist folglich 6×6 = 36 qdm („Quadratdezimeter“) groß.
- Eine quadratische 4 dm-Pizza ist 4×4 = 16 qdm groß.
Also:
- Zwei quadratische 4 dm-Pizzen sind zusammen 4×4 + 4×4 = 16 + 16 = 32 qdm groß.
- Eine quadratische 6 dm-Pizza ist 6×6 = 36 qdm groß.
Die Antwort auf die ursprüngliche Frage lautet daher: Zwei 40er Pizzen sind weniger als eine 60er Pizza. Und für die Lösung brauchten wir wirklich rein gar nichts außer das kleine Einmaleins, bzw. genauer gesagt: die Quadratzahlen von 4 und 6.
„Aber, aber, aber … !“
Ja, ja – „aber, aber, aber“: Wo kommt denn nun die Zahl Pi rein, und stimmt o.a. Milchmädchen- bzw. Pizzajungen-Rechnung auch noch für runde statt quadratische Pizzen?
OK – flugs mal herleiten: Nehmen wir an, wir haben eine quadratische Blechpizza mit 1 m Kantenlänge und folglich 1×1 = 1 qm Fläche. Und jetzt machen wir wieder den oben beschriebenen Schritt auf 2 m Kantenlänge – zur Wiederholung: Das sind 4 qm, denn wir legen ja vier 1×1 m Blechpizzen quadratisch aneinander.

Nun säbeln wir bei diesen vier Pizzen außen die Ecken rund. — Wie viel weniger ist das denn nun? Naja, wenn die Ecken fehlen, bleibt von den vier aneinander gelegten quadratischen Blechpizzen „irgendwie weniger als das Vierfache“ von eben. Aber wie viel weniger? Schätzung über den Daumen: Weniger als das Vierfache, aber mehr als das Dreifache.
Wie viel genau? Das kann man ausprobieren oder ausrechnen: Es ist das 3,14159-fache – das Pi-fache.
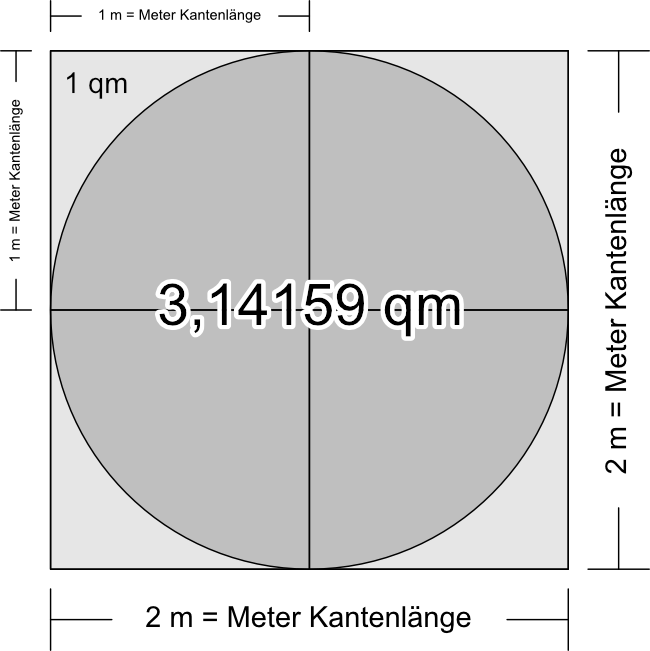
Noch einmal: Lege ich vier quadratische 1×1 m Pizzen quadratisch aneinander und säbele die vier Ecken rund, ist die verbleibende Fläche 3,14159 qm. — Mind = blown?
Und hier kommt der Karton: Auch dies gilt, egal ob wir die Mäusepizza mit vier aneinander gelegten quadratischen 1×1 cm-Pizzen an den Ecken rund säbeln, oder vier 1×1 dm-Pizzen oder vier 1×1 m-Pizzen: Am Ende sind wir immer beim 3,145159-fachen — exakt da kommt die Zahl Pi in die Pizza-Pie rein. Das ist quasi die Naturkonstante beim Absäbeln der Ecken von quadratischen Blechpizzen.
Und folglich hat das auch keinerlei Auswirkung auf die Daumenpeilung der Fläche einer 60er Pizza vs. zwei 40er Pizzen:
- Die 6 dm-Pizza entspricht vier quadratisch aneinander gelegten 3 dm-Blechpizzen, an denen wir die Ecken absäbeln.
- Eine 3 dm-Pizza hat 3×3 = 9 qdm, vier davon zusammen sind 4×9 = 36 (das hatten wir oben schon) – aber weil die Ecken abgesäbelt sind, ist es nicht das vierfache, sondern das Pi-fache … um genau zu sein: Etwas mehr als 28 qdm.
- Die 4 dm-Pizza entspricht vier quadratisch aneinander gelegten 2 dm-Blechpizzen, an denen wir die Ecken absäbeln.
- Eine 2 dm-Pizza hat 2×2 = 4 qdm, vier davon zusammen sind 4×4 = 16 (das hatten wir oben schon) – aber weil die Ecken abgesäbelt sind, ist es nicht das vierfache, sondern das Pi-fache … um genau zu sein: Etwa 12,5 qdm.
Ganz genau betrachtet sind zwei runde 40er Pizzen zusammen also etwa 2x 12,5 = 25 qdm, während eine runde 60er Pizza mit gut 28 qdm immer noch mehr ist.
Aber: Wir brauchen überhaupt keine genaue Zahl. Entscheidend ist, die Quadratzahlen miteinander zu vergleichen. — Das „Pi-fache“ bei runden statt quadratischen Pizzen ist für die Entscheidung hinsichtlich der Essensplanung für eine 60er vs. zwei 40er Pizzen vollkommen irrelevant.




Ahem… Das Verhältnis der Fläche eines Kreises zu seinem umschreibenden Quadrat ist konstant…
2*pi*r^2 / (2*r)^2 = pi/2
Deshalb haben die Quadratflächen der 60er und die der 40er das gleiche Verhältnis wie die Kreise:
60^2 > 2*40^2
Klingt mir etwas einfacher.
Uh, Faktor 2 zuviel! 😳
Das Verhältnis ist
Pi*r^2 / (2*r)^2 = pi/4
Ändert aber nix an der Grundaussage. 😎
@Michael – das ist ja alles bekannt und auch gut und richtig. Ich wollte aber in diesem Beitrag keine einzige Formel haben, und insbesondere auch dieses „Jetzt, wo wir was abschneiden, weniger als 4x soviel, aber wohl mehr als 3x soviel – wie viel denn? Ach so, 3,14159x so viel“ präsentieren.
Natürlich kann man sämtliches in Quadrate einbeschriebenen Kreise oder kreisumschreibenden Quadrate mitsamt Umfang vs. Radius vs. Fläche von 1001 Richtung beleuchten. Aber wie gesagt: Es ging mir hier um „Fläche wächst quadratisch – egal ob bei Blechpizza oder runder Pizza“. Und als Bonus noch konstruktiv die 3,14159 als „Blech- vs. runder Pizza-Naturkonstante“ einführen, die man aber für die Bewertung des Nährwertes gar nicht braucht.
Ohne Formeln. Ohne Exponenten. Ohne Brüche. Nur mit Quadratzahlen – und selbst mit dem Begriff kann man Mathephobiker schon genug erschrecken.